Table of Contents
FMCW Radar
The full form of FMCW Radar is frequency-modulated continuous–wave.
The CW radar is usually limited in its transmitted power by interference between the transmitter and receiver, which should operate simultaneously. This limits their sensitivity and range. Since there is no timing reference, CW radar systems cannot measure range which is the main disadvantage. The target range may be measured by changing the transmitter frequency linearly with time; this is called a frequency-modulated continuous–wave (FMCW) radar. In this radar system beat signal is produced when a frequency-modulated signal is mixed with an echo. For a relative motion, CW radars receive a signal which is shifted by fd but this is not helpful in determining the range from received echo signal. In FMCW radars, the transmitted signal is frequency modulated, so even if the target is stationary, the delayed signal is received with a different frequency. In FMCW radar the transmitted and received signal are mixed, which has information about the range and speed of the target.
A variety of modulations is possible; the transmitter frequency can slew up and down in the following manner:
- Sine wave
- Saw-tooth wave
- Triangle wave
- Square wave
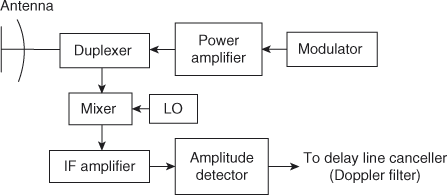
Block Diagram of FMCW Radar
The block diagram of FMCW Radar is shown in the figure below.
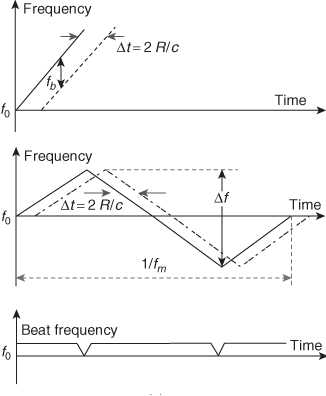
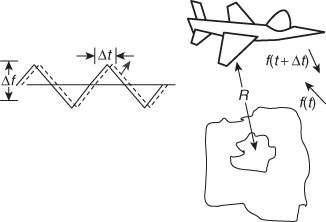
In the FMCW radar, the transmitter frequency is varied with respect to time. If the transmitter frequency increases linearly with time, and the target is present at range R, an echo signal is returned as shown in figure below. The time difference between the transmitted and received signals is \Delta t=2R/c if the transmitted and received signals are multiplied within a mixer, filtering out the high-frequency term of the output will give a beat frequency fb as shown in figure. The beat frequency has to be amplified and limited for eliminating any amplitude fluctuations, this is done by using an amplifier and a limiter. This is measured by the cycle-counting frequency meter which is calibrated in distance.
The above figure shows the frequency-time relationship in FMCW radar; where solid lines are represents transmitted signals and dashed or dot lines are represents echo signals. The above figure has three figures; the first figure shows the linear frequency modulation; the second figure shows the triangular modulation; the last or third figure shows the beat frequency
The beat frequency is a measure of the target’s range when there is no Doppler shift in the signal i.e., fb = fr (where fr is the beat frequency only due to the target’s range). If the slope of the frequency change in transmitted signal is mf, then we get
f_{b}=\Delta tm_{f}=\frac{2R}{c}m_{f}The above figure shows the frequency-time relationships in FMCW radar when the received signal is shifted in frequency by the Doppler effect. The first figure shows the transmitted and echo signal and another one shows the beat frequency.
Basically in any CW radar, only periodicity in modulation is essential because the frequency cannot be continuously changed in one direction. The modulation waveform can be of any shape. The above figure shows the triangular-frequency-modulated waveform and the resulted beat frequency using triangular modulation. mf is given as
m_{f}=\frac{\Delta f}{1/2f_{m}}=2f_{m}\Delta fThe beat frequency is uniform everywhere and changes only at turn-around region. If the variation of frequency is Δf, and the frequency is modulated at the rate fm, then the beat frequency where it is constant is arrived by substituting the value of mf in fb, then we get
f_{b}=\frac{4Rf_{m}\Delta f}{c}From this equation, the range R can also be determined from the measurement of the beat frequency. If
K=\frac{4f_{m}\Delta f}{c}Then
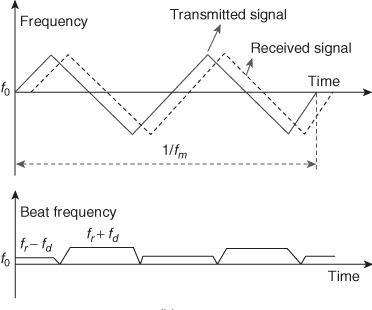
f_{b}=KRThe frequency-time plot of the transmitted and echo signals for the moving target is given in third figure. The situation described in second figure is the case when the target is stationary. If the target is moving, there will be a Doppler frequency shift superimposed to the beat frequency, and it should be considered in the demodulation. The Doppler frequency shifts the frequency-time plot of the echo (received) signal according to the relative direction of the target’s velocity.
The Doppler shift increases the beat frequency in one portion and decreases the beat frequency in the other portion of the frequency modulation cycle exchanging it between fb1 and fb2, where fb1 = fr − fd and fb2 = fr + fd. By switching the frequency counter for every half-cycle, the beat frequencies fb1 (up) and fb2 (down) of the cycle can be measured separately. Average of the two-beat frequencies gives the beat frequency, fr = ( fb1 + fb2)/2. Similarly Doppler frequency is given by, fd = ( fb1−fb2)/2.
FMCW Altimeter (Main Application of FMCW Radar)
A typical altimeter utilizes a transmitter power of about 1 to 2W and operates in C band. The target’s range is calculated based on the measured delay Δt between the transmitted signal and the received signal, whereas the frequency offset Δf gives the velocity. From Δt and Δf, the height of the aircraft can be calculated as shown in the figure below. The mixer output gives the frequency difference which is amplified and limited. This amplitude limited output is then fed to a frequency counter which in turn is fed to an indicator. The output thus obtained can be calibrated in feet or meters.
The advantage of the altimeter compared with the pulse radar is that measurement results are provided continuously.
Advantages of FMCW Radar
- High-resolution distance measurement suits well for imaging applications.
- Quick updating of measurement because of continuous transmitting signals.
- Functions well in all types of weather (rain, humidity, fog, and dusty) and atmospheric conditions, because electromagnetic radiations of short wavelength are used.
- Better in detecting tangential motion than Doppler-based systems.
Disadvantages of FMCW Radar
- Costlier than other competing technologies.
- Radar is most susceptible to interference from other radio devices.
- More computing power is required.
- It can be a disadvantage in defense applications because they can be easily blocked by electronic warfare systems.
Applications of FMCW Radar
- Used in high accuracy applications where repeatability and reliability are required because FMCW radars provide accurate range measurement.
- In transportation, it is used as automotive collision avoidance radars and marine radars.
- Because of its resistance to dust, steam, heat, these are mostly used in the blast furnace of a steel mill.