Table of Contents
Floating Point Numbers
Floating Point Numbers: All the numbering systems have been in the category of base r fixed point numbers. Fixed point number means that the fractional point (i.e., decimal point) is once finalized will remain fixed. The fractional point is fixed within each n bit number word. For example, if the system is 8 bit, and we decide that the fractional point is after the 5th bit then the binary format will be as under,

Here, it will be interesting to note that once, the number of bits are finalized for a particular system, we cannot change it abruptly. Hence, for above format, minimum number we can represent is (0)2 i.e.,
\begin{matrix} B_{4} & B_{3} & B_{2} & B_{1} & B_{0} & . & B_{-1} & B_{-2} & B_{-3} & = & (00000.000)_{2} \end{matrix}.
Maximum number that we can represent is \begin{matrix} B_{4} & B_{3} & B_{2} & B_{1} & B_{0} & . & B_{-1} & B_{-2} & B_{-3} & = & (11111.111)_{2} \end{matrix} i.e., (31.875)10.
To increase the range of the numbers to be represented, an obvious solution is to increase number of bits. Let us take an example for a 32 bit system. We take that integer part is of 32 bit. Then maximum number we can represent will be
232 – 1 = 4, 294, 967, 295 = 4.29 x 109.
But, if we want to represent Angstroms number i.e., 4.07 x 1026 A°, then it is not possible in 32 bit. Secondly minimum number that we can represent in above case is (0)10 = zero. But, if we want to represent suppose mass of electron in kilogram i.e., 1.67 x 10-27 kg, it is not possible. Here, we may argue to increase number of bits, but just increasing number of bits is not the solution because our system must support that many number of bits. Hence, finally the conclusion is, for a fixed point number representation, we cannot represent very large number and very small number.
Remedy
The remedy to this problem is to switch over to Scientific Notation. In scientific notation, the number is in the form of N = M x 10E, where M and E are fixed points numbers called, Mantissa and Exponent respectively. E is an integer that specifies the number of zeros to be appended to M, to obtain Floating point number N. Here, we may ask one question that why the Version of Scientific Number (notation) is called FLOATING POINT. To understand this, we shall take a simple example.
Let us consider the number (1000.234)10 This number can be represented as under:
| 1000234 x 10-3 1000234 x 10-2 1000234 x 10-1 1000234 x 100 | 1000234 x 101 10.00234 x 102 1.000234 x 103 0.100234 x 104 |
In the representation of (1000.234)10, we must have observed that the decimal point is not fixed as such. It can FLOAT from number to number depending upon the power of 10. Normally, in scientific notation, we represent numbers as M x BE. Therefore, depending upon our requirement, we set
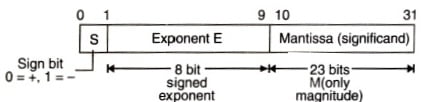
E and in M will allow decimal point to float. Therefore, it is called as floating point numbering system. In N = ± M x BE, B = base of floating point number system. We have taken base = 10 for decimal system. But, for binary number, it will be 2, B = 2. Let us see the format of floating point number system.
Format of floating point number
As shown in the above figure 32-bit format for floating-point. The sign S, indicates sign of mantissa. This bit is assigned left most position to maintain compatibility with the sign conversation for fixed-point binary numbers. Eight bits are used for exponent E, with the remaining 23 bits for mantissa. E represents signed binary integer, so that exponent value can range from – 128 to + 127. Floating-point numbers are standardized by IEEE. According to it, we have to represent the floating-point number in the form
±1. M x 2 E’ – 127 (Single Precision – 32 bit)
±1. M x 2E’ – 1023 (Double Precision – 64 bit)
Here M = Mantissa, E = E’ – 127. The format is shown in figure below.

We have, E = E’ – 127
Therefore E = E’ + 127
E = Exponent of number.
The range for E’ is 0 to 255.
Before we discuss exponent, first, let us understand what is 1. M. Whenever any number is given to us, to represent it in the floating-point number system, we have to bring it down to format 1. M. Say for example, where the number is given is 0.0110 x 26. Presently, the number has form 0. M M= 0110. But, we want 1. M. Hence, now, we shift the number to the left side till we get 1. M. While shifting the number we have to adjust the exponent also.
\left.\begin{matrix} 0.0110\times 2^{6} & \rightarrow & Actual number\\ 0.110 \times 2^{5} & \rightarrow & After 1^{st} shift\\ 1.10\times 2^{4} & \rightarrow & after 2^{nd} shift \end{matrix}\right\}Shift operationNow, we stop here as we have 1. M. Now, M = 10.
Therefore, the floating point number has the following parameters.

M= 10
S = plus (positive)
E’ = E + 127 = 4 + 127= 131 = (1 0000 1 1)2
Therefore, the floating-point number is as shown in the above figure. Tish figure shows the floating-point representation of 1.10 x 24.
Hence, finally number is (0 1 0 0 0 0 1 1 1 0 …)2. In hex, this number is (4 3 8 0 0 0 0 0)16.
De-normalized/Normalized Floating-Point Numbers
While representing 0.0110 x 26 number in floating-point, we have shifted the bits and adjusted exponent, till we get 1.M. The number we get after performing this operation is called Normalized Number i.e., brought down to our requirement. Secondly, if we see a floating-point number, it has format ± 1.M x 2E – 127. While representing it in IEEE format, we simply forget 1 in. 1.M. The answer for the same is, it is by default that we must have 1 before ‘fractional point’.
Therefore, the way we do not take the base (B) into account because it is the default, we do not take 1 into account, only while representing it. But, whenever, we perform any operation, it will be taken into account. From the above discussion, we must be now aware of the de-normalized number. A de-normalized number is a RAW number that does not follow the 1.M format.
Range of Floating Point Numbers
Each floating-point format (Single precision/double precision) has the capability to represent the number within a certain range. The generalized graphical representation is shown in the figure below.
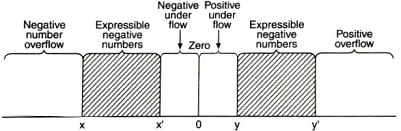
The above figure shows the numbers that can be expressed (+ve or -ve), by the shaded part. Below and above the shaded parts, numbers are not representable. Representable range of numbers are x – x and y – y.
Five regions are not included in the group.
- Negative numbers, those are under negative overflow.
- Negative numbers, those are under negative underflow.
- Zero
- Positive numbers those are under positive underflow.
- Positive numbers those are under positive overflow.
First, let us try to understand overflow/underflow.
Overflow occurs when an arithmetic operation results in magnitude greater than can be expressed with an exponent.
Underflow occurs when fractional part is too small. Under flow is less serious problem because the result can be approximated to zero. To represent 0, special bit pattern is designated. In IEEE format, when e = Exponent = 0 and significand (Mantissa) = 0, the number is zero.
In IEEE format, the largest exponent field E = (1 1 1 1 1 1 1 1)2, corresponds to 255, is reversed to denote infinite numbers that result from some types of overflow. In this standard, certain invalid bit combinations considered to be special, not a number (NAN category). The following table shows values in IEEE for single and double-precision numbers.
Table : Single Precision (32 bits)
| Exponent (E’) | Significand (Mantissa) | Value |
| 255 25 0 < e < 255 0 0 | ≠ 0 0 – ≠ 0 0 | NAN (-1)8 ∞ (-1)8 2E’-127 (1.M) (-1)8 2-126 (0.M) (-1)8 0 |
Table : Double Precision (64 bits)
| Exponent (E’) | Significand (Mantissa) | Value |
| 2047 2047 0 < e < 2047 0 0 | ≠ 0 0 – ≠ 0 0 | NAN (-1)8 ∞ (-1)8 2E’-1023 (1.M) (-1)8 2-1022 (0.M) (-1)8 0 |
Related Posts: