Table of Contents
Continuous Wave (CW) Radar
A continuous-wave (CW) radar system operating with a constant frequency can measure velocity, but not the range. A signal transmitted from an antenna which is having a certain frequency is reflected back by the target with a slight change in frequency, i.e. Doppler frequency shift. A comparison of the transmitted frequency with received frequency leads to the determination of the speed of the target (but not its range). CW radars make use of a sine wave of the form cos 2π f0t, where the echo from clutter (i.e. stationary targets) is concentrated at f0 in the frequency spectrum. The center frequency extracted from echoes of moving targets will be shifted by a frequency known as Doppler frequency, fd. Thus by measuring the frequency shift (f0~fd), target velocity can be determined accurately.
Doppler Effect
If either the transmitter or the receiver is in motion, resulting in an apparent shift in frequency, this is the Doppler effect and is the basis of the continuous-wave (CW) radar. Let us suppose the range of the target is R, and the wavelength is λ. By definition, each wavelength (λ) corresponds to a phase change of 2π radians. The total wavelength for the two-way propagation path (i.e. from radar to the target and its return to radar) is 2R/λ. Then the total phase change in the two-way path of the signal is given by,
\phi =2\pi \times \frac{2R}{\lambda} rad \phi = \frac{4\pi R}{\lambda} radLet us consider the target is in motion with respect to the radar, so when range (R) changes, the phase (ϕ) observed also changes. Then the rate of change of phase \left ( \frac{d\phi }{dt} \right ) is referred to as angular frequency, ωd. Therefore, the angular frequency can be obtained by differentiating the above equation with respect to time.
\omega _{d}=2\pi f_{d}=\frac{d\phi }{dt}=\frac{4\pi }{\lambda }\left ( \frac{dR}{dt} \right )=\frac{4\pi \nu _{r}}{\lambda }where, \nu _{r}= radial velocity = \frac{dR}{dt} (knots)
Hence the Doppler frequency is given by
f_{d}= \frac{2 \nu _{r}}{\lambda }Usually, radial velocity is given in the units of knots (or kt), wavelength (λ) is in meters, then the Doppler frequency is measured in Hertz (Hz). Thus, the above equation can be written as,
f_{d}= \frac{1.03 \nu _{r}\left ( kt \right )}{\lambda\left ( m \right ) }where, 1 knot = 1.852 Km/hr or 0.514 m/sec.
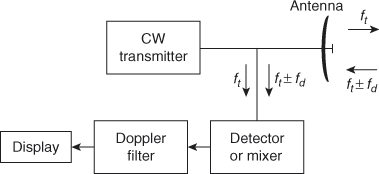
Block Diagram of continuous-wave (CW) radar
The block diagram of the simple continuous-wave (CW) radar is shown in the figure below. The CW radar uses the Doppler frequency shift principle to identify the moving target.
Working of continuous-wave (CW) radar
The main use of the Doppler filter is to filter and eliminate the echoes from the stationary targets, and also amplifies the weak Doppler echo signal so that it can be identified in the display device. These weak signals are filtered in the frequency domain in the filter. The mixer mixes the echo signal at a frequency ft ± fd with the corresponding transmitted signal (or reference signal), ft which is the frequency of continuous sinusoidal oscillations. While transmission, the antenna radiates a continuous sinusoidal oscillation at a frequency, ft.
A portion of this radiated energy intercepted by the target and the re-radiated energy is collected by the receiver antenna. If we consider the target is moving with a velocity vr, relative to the radar, then the signal received shifts in frequency from the transmitted frequency by ft ± fd. If the target is moving towards the radar, then the frequency shift is given by ft + fd. Thus, the echo signal from a closer target has a higher frequency than that was transmitted. If the target is moving away from the radar, then the frequency shift is given by ft −fd. In order to use the Doppler frequency shift, the radar should be capable to distinguish the difference between the received echo signal and the transmitted signal.
In the CW radar, each target velocity produces a single distinctive Doppler frequency of the CW carrier. This results in clear Doppler measurement, which is the main advantage in CW radar. Whereas there is any uncertainty in the measurement of range using CW radar because all the returned waveforms are continuous and hence the radar is not able to differentiate between the different echoes received. Most of the modern radars utilize a pulse waveform technology, in which a single antenna is used for both transmitting and receiving functions.
Advantages of CW Doppler Radar
- It is simple, inexpensive, easy to maintain, and fully automated.
- It needs low power and is compact in size.
- Peak power is less, as the duty cycle is unity.
- Stationary objects do not affect the performance of the radar.
Disadvantages of CW Doppler Radar
- There is a limitation by the power in the maximum range of the CW radar.
- Maximum power depends on the amount of isolation and the transmitter noise, which affects the receiver sensitivity.
- The target range cannot be obtained by the CW Doppler radar.
- When there is a number of targets there is a possibility of ambiguity.
Applications of CW Doppler Radar:
CW Doppler radars are used to determine velocity information but not range; for instance,
- It can be used in cricket to measure ball speed
- CW radar can be used in traffic to monitor traffic
- In police radar to catch cars exceeding the speed limit
- It can be used in aircraft navigation to measure the speed
- In planes as a rate-of-climb indicator for vertical takeoff planes