Introduction to Hazards

Hazards

The term hazards implies the unwanted switching transients or false outputs or glitches that appear at the output of a circuit. These transient false outputs are because of the finite propagation delay times of the components along different paths within a network.

In fact, difference in the propagation delays corresponding to different signal paths result in hazards.

A hazards may be defined as the actual or potential malfunction of a logic network during the transition between two input states when a single variable changes. Malfunctioning means any deviation from the intended response.

In case of combinational circuits, the hazards result in a false output value. However, if each combinational circuit is used as a building block of an asynchronous sequential circuit, then it shall result in a transition to incorrect stable state.

Flip Flop | Types, Truth Table, Applications

Conversion of Flip-flops from One to Another

Classification of Hazards

The hazards may be classified in 3-types as shown in figure below.

Static 1 Hazard

If the output is supposed to be 1 (HIGH) but due to difference in propagation delay if it becomes 0 (LOW) for a short time, then a static-1 hazard is said to have taken place.

Static 0 Hazard

A static 0 hazard is said to have taken place if the circuit output produces a short duration HIGH pulse when actually, it is supposed to product a LOW (0) output.

Dynamic Hazard

In the static hazards, the output changes twice. But as shown in figure 13.1, if the output changes for 3 or more times when it is supposed to change only once from 0 to 1 or from 1 to 0, then the dynamic hazard is said to have taken place.

Static Hazards

A static hazard in a logic network may be defined as a transient change of an output value which is supposed to remain fixed during the transition between two input states differing in the value of only one variable. When the output is supposed to remain at 0, but it is likely to go high (to logic 1) momentarily during the transition of input states, then the hazard is called as a static 0 hazard.

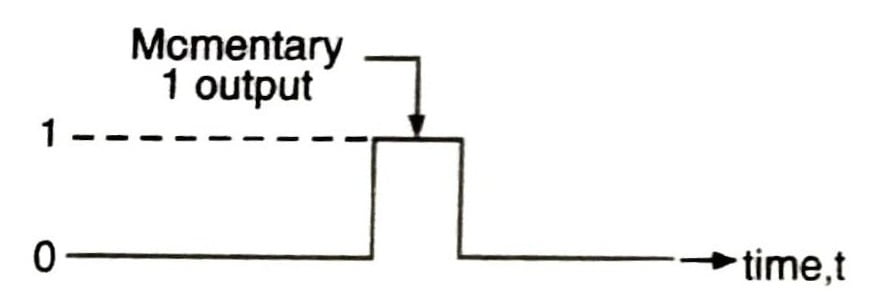
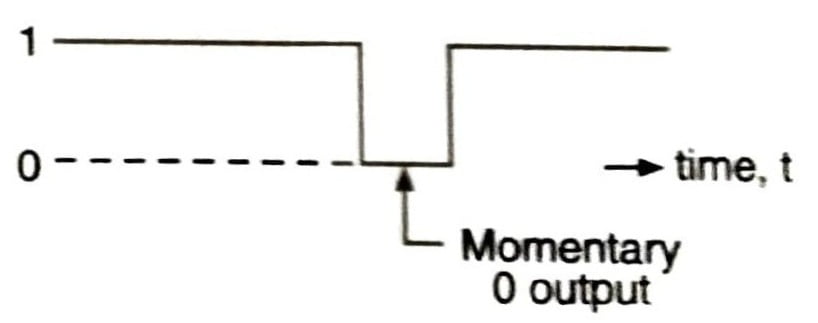
On the other hand, if a momentary 0 is likely to occur in the output when it is expected to remain 1, then the hazard is called as a static-1 hazard.

Effects of Hazards

The effect of seriousness of hazards is dependent on the devices or systems which receive the momentary transient signals.

In case of asynchronous sequential networks, the presence of hazards can cause the network to malfunction.

Detection of Static Hazards

Static hazards may be detected with the help of Boolean algebraic expressions in which a variable and its complement are treated as different i.e. as non related variables. This is because, under the transient conditions, a variable and its complement can momentarily have the same logic value. Just to detect static hazards, the Boolean expression of the network is first written in the form which is in the one to one correspondence with the network.

This expression is then manipulated into a SOP form, for the detection of static-1 hazards. The expression is written in the POS form, for the detection of static-0 hazards.

All the theorems except for the following, can be used for manipulation,

A\bar{A}=0, A+\bar{A}=1, A+\bar{A}B=A+B

This is because we have to treat A and A as different variables, in transient analysis. However, the laws such as A + AB = A and A (A + B) = A are to be employed.

The resulting SOP or POS expressions after manipulation are known as transient normal formulas. The product terms in the SOP equations are called as 1-terms and the sum terms in the POS equations are called as 0-terms.

SOP expression is also known as transient disjunctive formula whereas the POS expression is also called as transient conjunctive formula. 

Use of Transient Disjunctive (SOP) Formula

Each 1-term in the transient disjunctive (SOP) formula corresponds to a path through the network that provides a 1 output.

From the K-map for SOP formula we can conclude as under: If two adjacent 1-cells on the map occur within a subcube for a single 1-term, then the output of the network must have the value 1 during the transition between the corresponding input states since only one path is involved. On the other hand, if there are two adjacent 1-cells on the map which do not occur within a subcube of a single 1 term, then there has to be a path change for the 1 output of the network due to change in the value of single variable.

The two paths involved correspond to the two different 1-term subcubes. In the process of switching from one path to the other, a momentary 0 output may occur if the original term producing a 1 output changes to zero before the term originally producing a 1 output changes to 0 before the term originally producing a 0 output changes to 1. This means that static 1 hazard exists.

How to detect static-1 hazards ? We can detect static-1 hazard by plotting all the 1-terms not containing a complementary pair of literals in a transient disjunctive normal formula and then by noting if each pair of adjacent 1-cell is contained in some single subcube.

Use of Transient Conjunctive Normal Expression (POS Form)

1. The 0-terms of the transient conjunctive normal expression or the POS expression can be used to detect the static 0-hazards.
2. A 0 term has a zero value only when each of its literals has the value 0. Therefore, each 0 term corresponds to a set of input states which causes the output of a combinational circuit to be 0.
3. We can detect a static 0 hazard by mapping all the 0-terms that do not contain a pair of complementary literals and then by noting if there are any two adjacent 0s which  are not contained in some single 0-term subcube (group).

Relation between static 0-hazard and 1-terms

We have used the 0-terms for detecting the static 0-hazards. But there is an observation about the non-existence of static 0-hazards and 1-terms. The observation is that, if no 1-term in the transient disjunctive normal formula (SOP expression) contains a variable and its complement, then the network will not have any static 0-hazards, in a two level realization, unless there are gates having a pair of complementary literals as their inputs. Therefore, inclusion of such gates must be avoided.

Similar, conclusion can be drawn about the relation between the 0-terms in the POS formula and the existence of static 1 hazard i.e. a network will have no static-1 hazards if there are no 0-terms containing a pair of complementary literals.

Elimination of Static Hazards

To eliminate the static hazards, we have to use the additional logic to provide the holding action which is necessary for eliminating the static hazards. This additional logic is determined by grouping the two adjacent l’s or 0’s which are responsible for static hazard, into a common subcube. This has been illustrated in the next example.

Dynamic Hazards

The other type of hazard associated with the combinational networks is called as a dynamic hazard. It also has the same effect as that of static hazards i.e. false output. The Dynamic hazards occur when the output of the circuit is to change from one logic level to the other one but a momentary false output signal occurs during the transient behaviour.

Dynamic Hazard: Definition

We can define the dynamic hazard as a transient change which occurs three or more times at the output of a logic circuit, when the output is supposed to change only once during the transition between two inputs states which differ in the value of one variable.

Hazardfree Combinational Networks

It is possible to prove that if we implement a combinational circuit directly from the disjunctive normal (SOP) expression with no product terms containing a variable and its complement and in which additional terms are included to avoid static 1-hazard, then such a network is free of static 0-hazards as well as dynamic hazards.

Similarly, if we implement a combinational circuit directly from a conjunctive normal (POS) expression with no sum terms containing a variable and its complement and additional terms are included to avoid static 0-hazards, then such a network is free of static 1-hazards as well as dynamic hazards.

Combinational circuits free of static and dynamic hazards are called as a hazardfree circuit.

Essential Hazards

A fundamental mode asynchronous circuit may malfunction even after avoiding the critic races and eliminating static and dynamic hazards.

This is because of the fact that fundamental mode asynchronous circuits are prone to another type of hazard, known as the essential hazard. This is another kind of hazard which is likely to occur in the asynchronous sequential circuits. It results from unequal delays along two or more paths with originate from the same point. If such thing occurs in the feedback path of the asynchronous sequential circuit then it is known as essential hazard, since for asynchronous sequential circuits, the feedback loop is essential. It is possible to eliminate such hazards by adjusting the delays of the involved paths so that they become exactly equal.

Because of essential hazards, the asynchronous sequential circuit may become stable in some other state than intended. The existence of essential hazard may be directly from the flow table.