Introduction to Number Systems

Number System: A number is a collection of digits and it is represented by (N)_b, where b is the base and N is the number. The base or radix of a number system is defined as the number of different possible symbols hold by a digit in each position in the number system. A number, in general, has two parts – integer and fractional, set apart by a radix point.

A number system is a basis for counting various items. On hearing the word ‘number’, all of us immediately think of the familiar decimal number system with its 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

As a matter of fact, modern computers communicate and operate with binary numbers which use only the digits 0 and 1. Let us consider decimal number 18. This number is represented in binary as 10010. In the example, if a decimal number is considered, we require only two digits to represent the number, whereas if the binary number is considered, we require five digits. Therefore we can say that, when decimal quantities are represented in the binary form, they take more digits.

For large decimal numbers, people have to deal with very large binary strings, and therefore, they do not like working with binary numbers. This fact gave rise to three new number systems: Octal, Hexadecimal, and Binary Coded Decimal (BCD). These number systems represent the binary number in a compressed form. Therefore, these number systems are now widely used to compress long strings of binary numbers.

Important Points to Define a Number System

To define any number system, we have to specify following aspects:

• The base of the number systems such as 2, 8. 10, or 16.
• The base decides the total number of digits available in that number system. For example, if the base is 2, we have 2-digits (0 and 1), if the base is 10, we have 10-digits (0 through 9), and so on. Therefore, the total number of digits available in the number system is equal to the base of the number system.
• The first digit in the number systems is always zero (0) and the last digit in the number systems is always base – 1. As an example, in the decimal system, last digit is 9 (10-1).

Important Terms of Number Systems

It will be interesting to know that all the numbering systems have a few common aspects as under:

Base or Radix

The number of values that a digit (one character) can assume is equal to the base of the system. It is also called as the Radix of the system. It is denoted by r. For example, for a decimal system, the base is 10 hence every digit can assume 10 values (0, 1, 2,   9).

The largest value of a digit is always one less than the base, for example, the largest digit in a decimal system is 9. (One less than the base 10).

Each digit position (i.e., place) represents a different multiple of base: This means that the numbers have positional importance. For example, let us consider the decimal number (349.25)₁₀.

Hence, we can implement a common rule for all the numbering systems as under.

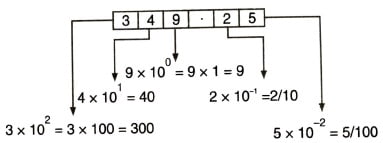
For a general number, we have to multiply each digit by some power of base (B) or radix as shown in the figure below.

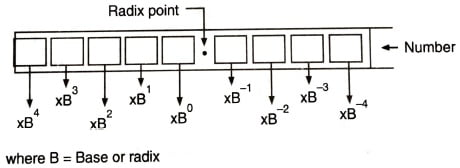
Column Numbers

The column number is the number assigned to the digits placed in relation to the radix point. Column numbers to the left of the radix point start with 0 and go up (0, 1, 2, ….) as shown in the above figure. Column numbers to the right of the radix point start from -1 and become more and more negative (-1, -2, -3, -4, …) as shown in the figure.

Various Numbering Systems

Various numbering systems used in practice and their bases are as shown below in table form.

S.No.	Name of number system	Base/ Radix
1.	Binary	2
2.	Octal	8
3.	Decimal	10
4.	Duodecimal	12
5.	Hexadecimal	16

Table: illustrates base, 1st digit. last digit and available digits in various number systems.

S.No.	Number System	Base	First Digit	Last Digit	All Digits/ Characters
1.	Binary	2	0	1	0, 1
2.	Octal	8	0	7	0, 1, 2, 3, 4, 5, 6, 7
3.	Decimal	10	0	9	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
4.	Hexadecimal	16	0	F	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Important Point: In hexadecimal number system, meaning of A = 10, B = 11, C = 12, D = 13, E = 14 and F = 15.

Decimal Number System

Before considering any number system, let us consider familiar decimal number system. In decimal number system, we can express any decimal number in units, tens, hundreds, thousands and so on.

When we write a decimal number, say, 5678.9, we know it can be represented as under

5000 + 600 + 70 + 8 + 0.9 = 5678.9

The decimal number 5678.9 can also be written as (5678.9)_10, where the 10 subscript indicates the radix or base.

In power of 10, we can write as under:

This means that the position of a digit with reference to the decimal point determines its value/weight. The sum of all the digits multiplied by their weights gives the total number being represented. The leftmost digit, which has the greatest weight is called the Most Significant Digit and the rightmost digit, which has the least weight, is called the Least Significant Digit. The figure is shown below decimal digit and their weights expressed as a power of 10.

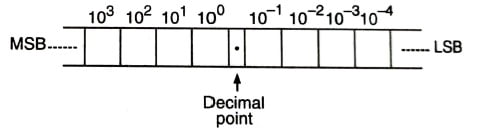
Binary Number System

We know that the decimal system with its ten digits is a base-ten system. Similarly, a binary system with its two digits is a base-two system. The two binary digits (bits) are 1 and 0. Like a digital system, in binary systems, each binary digit commonly known as the bit has its own value or weight. However, in a binary system, weight is expressed as a power of 2, as shown in the figure below.

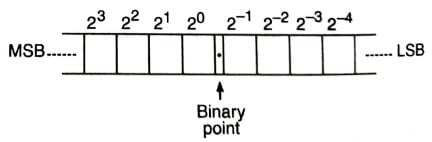
Octal Number System

We know that the base of the decimal number system is 10 because it uses the digits 0 to 9, and the base of a binary number system is 2 because it uses digits 0 and 1. The octal number system uses the first eight digits of the decimal number system: 0, 1, 2, 3, 4, 5, 6, and 7. As it uses 8 digits, its base is 8.

Hexadecimal Number System

The hexadecimal number system has a base of 16 having 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. It is another number system that is particularly useful for human communications with a computer. Although it is somewhat more difficult to interpret than the octal number system, it has become the most popular. Since its base is a power of 2 (2⁴), it is easy to convert hexadecimal numbers to binary and vice versa.

Relationship between Decimal, Binary and Hexadecimal Numbers

The table is shown the relationship between decimal, binary and hexadecimal. Note that each hexadecimal digit represents a group of four binary digits, called a nibble, that are fundamental parts of larger binary words.

Relationship between decimal, binary and hexadecimal numbers

S.No.	Decimal	Binary	Hexadecimal
1.	0	0000	0
2.	1	0001	1
3.	2	0010	2
4.	3	0011	3
5.	4	0100	4
6.	5	0101	5
7.	6	0110	6
8.	7	0111	7
9.	8	1000	8
10.	9	1001	9
11.	10	1010	A
12.	11	1011	B
13.	12	1100	C
14.	13	1101	D
15.	14	1110	E
16.	15	1111	F

Related Posts:

Difference Between Mealy And Moore Machine

Multivibrator: Bistable, Monostable, Astable