Table of Contents
Frequency Response Analysis
Definition of Frequency Response Analysis: The steady-state response of a system to a purely sinusoidal input is defined as the frequency response of a system. In such a method frequency of the input signal is to be varied over a certain range and the resulting response of the system is to be studied. Such a response is called frequency response.
Frequency response of the system is defined as the response of the system when standard sinusoidal signals are applied to it with constant amplitude over a range of frequencies. The frequency response indicates the steady-state response of a system to a sinusoidal input. The characteristics and performance of the industrial control system are analysed by using the frequency response techniques. Frequency response analysis is used in numerous systems and components such as audio and video amplifiers, speakers, sound cards and servomotors. The different techniques available for frequency response analysis lend themselves to a simplest procedure for experimental testing and analysis. In addition, the stability and relative stability of the system for the sinusoidal input can be analysed by using different frequency plots.
You may like to know about Concept of Stability | Control System
Frequency Response Representation
The frequency response analysis of a system is used to determine the system gain and phase angle of the system at different frequencies. Hence, the system gain and phase angle can be represented either in a tabular form or graphical form.
Tabular form: It is useful in representing the system gain and phase angle of a system at different frequencies only if the data set is relatively small. It is also useful in experimental measurement.
Graphical form: It provides a convenient way to view the frequency response data. There are many ways of representing the frequency response in the graphical form.
Determination of Frequency Response
The frequency response analysis of a system can be determined using the following determination methods.
Experimental determination of frequency response
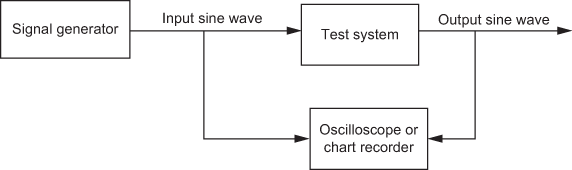
This method is used only when the system transfer function is not known. This method is used for a plant testing and verification of the plant model. Determining the frequency response of a the small system experimentally in a laboratory environment is not very difficult. A typical set-up for the experimental determination of the frequency response is shown in figure.
The requirement for determining frequency response varies for different systems. The general requirements for determining the frequency response of systems are power supply, signal generator and a chart recorder or dual trace oscilloscope. The experimental set-up varies depending on the test systems.
The steps to be followed for determining the frequency response are:
- Test frequency range and input signal amplitude are established.
- Sinusoidal signal with low frequency is applied and sufficient time is allowed for settling of transients present in the system.
- After a stable output is reached, using the input and output waveforms, the system gain and phase angle are determined.
- The same procedure can be applied for the input signal with different frequencies and the frequency response analysis of the system can be determined.
Thus, the frequency response of the system whose transfer function is not known can be determined.
Mathematical evaluation of frequency response
This method is applicable to the system whose transfer function is known. In this method, by substituting s=jω, the transfer function is considered to be a function of frequency and it is treated as a complex variable. The system gain and phase angle at a particular frequency is same as the magnitude and phase angle of the complex number.
The mathematical procedure for determining the frequency response of simple and complex transfer functions are given below:
Simple transfer function
- Choose the frequency for which the frequency response has to be determined.
- Substitute s=jω in the given transfer function.
- Convert the resultant complex number into a polar form.
- Substitute the chosen frequency ω in the above equation and determine the magnitude and angle of the complex number.
- Then, the system gain and phase angle at that particular frequency is determined.
- Repeat the above steps for different frequencies and the corresponding system gain and the phase angle can be tabulated.
Complex transfer function
A complex transfer function can be separated in two simple transfer functions and each simple transfer function can be converted into the polar form. The complex number in polar form allows easier manipulation of magnitude and angle. The procedure is as follows:
- Convert the complex transfer function into a product of simple transfer functions.
- For each simple transfer function, follow the steps that have been discussed earlier to determine the individual magnitude and angle of the simple transfer functions.
- Then, the overall gain and phase angle of the complex transfer function at a particular frequency can be obtained by multiplying the individual gain and adding the phase angles, respectively.
- The above steps can be repeated for different frequencies and the system gain and phase angle can be determined.
Advantages of Frequency Response Analysis
The time response of the system can be obtained only if the transfer function of the system is known earlier, which is always not possible. But it is possible to obtain frequency response of the system even though the transfer function of the system is not known. The reasons for determining the frequency response of the system are:
- Analytically, it is more difficult to determine the time response of the system for higher-order systems.
- As there exists numerous ways of designing a control system to meet the time-domain performance specifications, it becomes difficult for the designer to choose a suitable design for a particular system.
- The transfer function of a higher-order system can be identified by computing the frequency response of the system over a wide range of frequencies ω.
- The time-domain specifications of a system can be met by using the frequency domain specifications as a correlation exists between the frequency response and time response of a system.
- The stability of a non-linear system can be analysed by the frequency response analysis.
- The transfer function of a higher-order system can be obtained using frequency response analysis which makes use of physical data when it is difficult to obtain using differential equations.
- The frequency response analysis can be applied to the system that has no rational transfer function (i.e., a system with transportation lag).
- It can be applied to the system even when the input is not deterministic.
- The frequency response analysis is very convenient in measuring the system sensitivity to noise and parameter variations.
- In frequency response analysis, stability and relative stability of a system can be analysed without evaluating the roots of the characteristic equation of the system.
- The frequency response analysis is simple and accurate.
Disadvantages of Frequency Response Analysis
The disadvantages of frequency response analysis are:
- Frequency response analysis is not recommended for the system with very large time constants.
- It is not useful for non-interruptible systems.
- It can generally be applied only to linear systems. When this approach is applied to a non-linear system, the result obtained is not exact.
- It is considered outdated when compared with the methods developed for digital computers and modelling.