Transfer function & State-space
Transfer function & State-space: In Control system engineering there are 2 approaches to the analysis & design of the control system: 1. The transfer function or conventional approach, 2. The state-space or modern approach
The transfer function or conventional approach used to study the behavior of linear time-invariant control systems uses the time domain or frequency domain methods. In all these methods, the systems are modeled using the transfer function approach, which is the ratio of Laplace transform of output to input, neglecting all the initial conditions. Thus this conventional analysis faces all the limitations associated with the transfer function approach. Some of its limitations can be stated as:
- The transfer function is defined only under zero initial conditions.
- It is only applicable to linear time-invariant systems and generally restricted to single-input single-output (SISO) systems.
- The transfer function gives output for a certain input and provides no information about the internal state of the system.
- It gives an analysis of the system for some specific types of inputs like Step, Ramp, etc.
- It is only applicable to Linear Time-Invariant Systems.
- The classical methods like Root locus, Bode plot, etc. are basically trial and error procedures that fail to give the optimal solution required.
Hence it is absolutely necessary to use a method of analyzing systems that overcome most of the above-said difficulties.
The concept of the total internal state of the system considering all initial conditions. This technique which uses the concept of state is called State Variable Analysis or State Space Analysis. It is essentially a time-domain approach but it has a number of advantages compared to conventional methods of analysis.
In this post, the major differences between the convetional (transfer function) approach & the modern (state-space) method discussed.
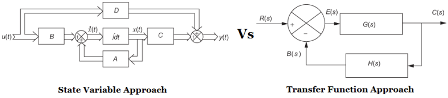
Difference between transfer function and state-space Approach
| S. No. | Transfer Function Approach | State Variable Approach |
| 1 | Transfer Function approach is also called conventional approach or classical approach. | State variable approach is called modern approch. |
| 2 | It is applicable to Linear Time-Invariant systems. it is generally limited to single input single output systems. | It is applicable to Linear as well as Non-Linear, Time Variant as well as Time Invariant, Single Input Single Output as well as Multi Input Multi Output Systems. |
| 3 | In this initial conditions are neglected. | They are considered. |
| 4 | It is basically a frequency domain approach. | It is a time domain approach. |
| 5 | It is based on trial & error procedure. | It is not based on trial & error procedure. |
| 6 | Only input, output & error signals are considered. The input & output variables must be measurable. | State variable need not represent physical variables. They need not be measurable & observable. |
| 7 | Internal variables cannot be feedback. | State variables can be feedback. |
| 8 | Transfer function of a system is unique. | State model of a system is not unique. |