Table of Contents
Binary Adder
The binary adder is a combinational circuit that can perform summation of the input binary numbers. The most common or basic arithmetic operation is the addition of binary digits. A combination circuit which performs the additions of two bits is a called a half adder while that performs the addition of three bits is a full adder.

Half Adder
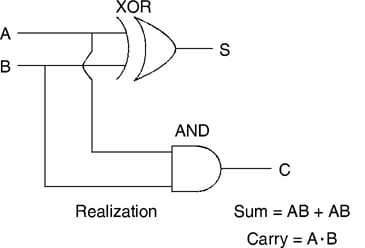
The Half adder is the simplest of all adder circuits. Half adder is a combinational arithmetic circuit that adds two numbers and produces a sum bit (S) and carry bit (C) both as the output. Let us consider two inputs bits A and B, then sum bit (S) is the X-OR of A and B and the carry bit (C) will be the AND of A and B. It is evident from the function of a half adder that it requires one X-OR gate and one AND gate for its construction. Let us first consider the addition of single bits.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
These are the least possible single-bit combinations. But it is noticed that the output as a result of the addition of 1 + 1 results in 10. This can be solved using an EXOR Gate, or the sum result must be re-written as a 2-bit output. Thus, the above equations can be written as
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Half Adder Truth Table
Here the output “1” of “10” becomes the carry-out. The “SUM” is the normal output and “CARRY” is the carry-out. Though the half adder is the simplest adder circuit, it has a major disadvantage. A half adder can add only two input bits (A and B) and is not affected by the carry of the input. As a result, if the input that is given to a half adder has a carry, then it will be neglected and it adds only the bits A and B. But this results in an incomplete binary addition and hence it gets its name a half adder. The truth table of half adder is shown in the above table.
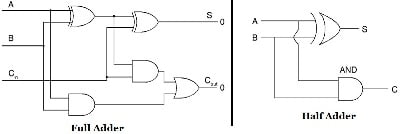
Full Adder
The full adder is a much complex adder circuit compared to the half adder. The major difference between a half adder and a full adder is the number of input terminals that are fed to the adder circuit. The full adder has three inputs and two outputs. The first two inputs are A and B and the third input is an input carry designated as CIN. The full adder is designed in such a way that it can take in eight bits together to create a byte-wide adder and cascade the carry bit from one adder to the next. The output carry is designated as COUT and the normal output is designated as S. Consider the following truth table for a full adder.
Full Adder Truth Table

The output S is an XOR between the input A and the half adder sum output with B and CIN inputs. The COUT will only be true if any of the two inputs out of the three are HIGH. Thus, a full adder circuit can be implemented with the help of two half adder circuits. The function of the first half adder is to add the inputs A and B to produce a partial sum. The second half adder adds the output of the first adder and the CIN to get the final output (S). If there will be an output carry. Thus COUT will be an OR function of the half adder carry outputs. The sum of the products (SOP) for the above truth table with sum Sn and carry Cn is given as:

The full adder circuit is shown in figure below. It comprises of two XOR gates and two AND gates and one OR gate. It can also be constructed using a NAND gate by employing double complement method.

Though the implementation of larger logic diagrams is possible with the above full adder logic, a simpler symbol is mostly used to represent the operation. The simple one bit symbol of a full adder is as shown in figure below.

The Block diagram of full adder implementation via a pair of half adders is as shown in figure below.

Multi-bit Adder using Full Adder
The above-mentioned adder is used to sum up to 2 bits together taking a carry from the next lower order of magnitude and sending a carry to the next higher order of magnitude. For a multi-bit operation, each bit must be represented by a full adder and all the bits must be added simultaneously. Thus, to add two 8-bit numbers, we need 8 full adders which can be formed by cascading two of the 4-bit blocks. The addition of two 4-bit numbers is shown below.